[TOC]
Neural Architecture Search with Reinforcement Learning
Abstract
Use a recurrent network to generate the model descriptions of neural networks and train this RNN with reinforcement learning to maximize the expected accuracy of the generated architectures on a validation set
Introduction
A gradient-based method for finding architecture
Work is based on the observation that the structure and connectivity of a neural network can be typically specified by a variable-length string. Use a recurrent network, the controller, to generate such string
Reward: result in an accuracy on a validation set
Controller will give higher probabilities to architectures that receive high accuracies
Related work
Hyperparameter optimization
Existed work only search models from a fixed-length space. They often work better if they are supplied with a good initial model.
Bayesian optimization models could search non fixed length architectures, but less general and less flexible than this one
Modern neuro-evolution algorithm
less practical at a large scale
slow or require many heuristics to work well
The controller in NAS is auto-regressive, which means it predicts hyperparameters one a time, conditioned on previous predictions
Method learns directly from the reward signal without any supervised bootstrapping
The idea of learning to learn or meta-learning
Methods
Generate model description with a controller recurrent neural network
Controller to generate architectural hyperparameters of neural networks: RNN
Use their controller to generate their parameters as a sequence of tokens
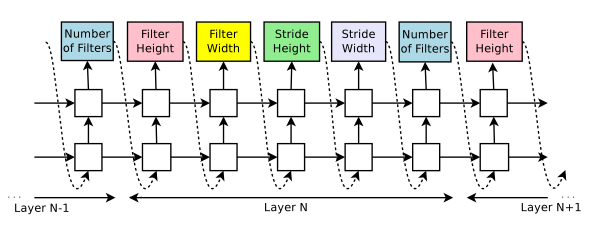
Every prediction is carried out by a softmax classifier and then fed into the next time step as input
Generating an architecture stops if the number of layers exceeds a certain value
At convergence, the accuracy of the network on a held-out validation set is recorded
The parameters of controller RNN: $\theta_c$
Training with Reinforce
The list of tokens: a list of action $a_{1:T}$
$R$: reward signal, accuracy on a hold-out dataset
PG in RL:
$$
J(\theta)=E_{p(a_{1:T};\theta_c)}[R]
$$
$$
\nabla_{\theta_c} J(\theta_c)=\sum_{t=1}^TE_{p(a_{1:T};\theta_c)}[\nabla_{\theta_c}logP(a_t|a_{(t-1):1};\theta_c)R]
$$
$$
\frac{1}{m}\sum_{k=1}^m\sum_{t=1}^T\nabla_{\theta_c}logP(a_t|a_{(t-1):1};\theta_c)R_k
$$
m: number of different architectures
T: number of hyperparameters controller has to predict to design a nn architecture
Baseline function, address unbiased estimate
$$
\frac{1}{m}\sum_{k=1}^m\sum_{t=1}^T\nabla_{\theta_c}logP(a_t|a_{(t-1):1};\theta_c)(R_k-b)
$$
baseline b is an exponential moving average of the previous architecture accuracies
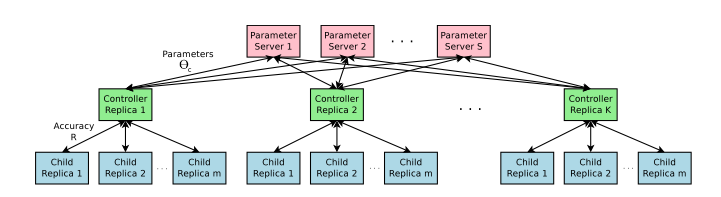
Accelerate training with parallelism and Asynchronous updates
Distributed training and asynchronous parameters updates to speed up the learning process of the controller
Each controller replica samples m different child architectures that are trained in parallel
Each controller replica then samples m architectures and run the multiple child models in parallel
The controller then collects gradients according to the results of that minibatch of m architectures at convergence and sends them to the parameter server in order to update the weights across all controller replicas
Convergence of each child network is reached when its training exceeds a certain number of epochs
Increase architecture complexity with skip connections and other layer types
Widen the search space, using skip connections or branch layers
built upon the attention mechanism
At each layer, an anchor pointer which has N-1 content-based sigmoids to indicate the previous layers that need to be connected
Each sigmoid is a function of the current hiddenstate of the controller and the previous hiddenstates of the previous N-1 anchor points
$$
P(\text{layer j is an input to layer i})=sigmoid(v^T tanh(W_{prev}h_j+W_{curr}h_i))
$$
Then sample from these sigmoids to decide what previous layers to be used as inputs to the current layer
$W_{prev}, W_{curr}, v$ are trainable parameters
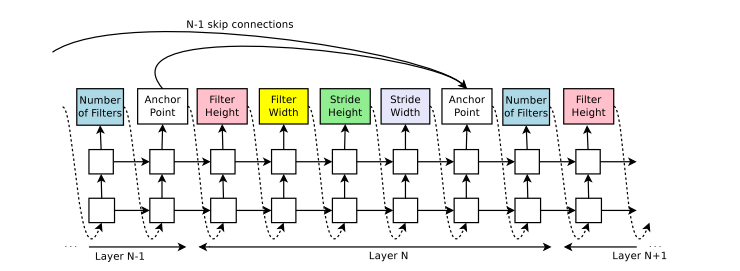
If one layer has many input layers then all input layers are concatenated in the depth dimension. Skip connections can cause “compilation failures” where one layer is not compatible with another layer, or one may not have any input or output. Employ three simple techniques
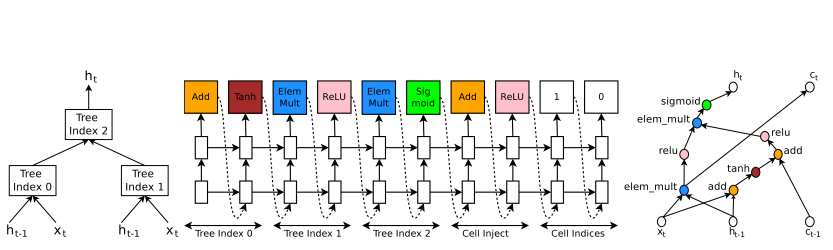
Generate recurrent cell architectures
The computation for basic RNN and LSTM cells can be generalized as a tree of steps and take $x_t$ and $h_{t-1}$ as inputs and produce $h_t$ as final output
Index the node in the tree in an order so that the controller RNN can visit each node one by one and label the needed hyperparameters
Experiments and results
Learning convolution architecture for CIFAR-10
Dataset
Search space
convolution layers, rectified linear units, non-linearities, batch normalization, skip connection between layers
Training details
Controller: 2 layer LSTM with 35 hidden units
Adam, lr = 0.0006
server shard S: 20, controller replicas K:100, chlid replicas: 8
800 networks being trained on 800 GPUs concurrently at any time
Once the controller RNN samples an architecture, a child model is constructed and trained for 50 epochs. The reward used for updating the controller is the maximum validation accuracy of the last 5 epochs cubed
During training, use a schedule of increasing number of layers in the child networks as training progresses
After finding the architecture that achieves the best validation accuracy, run a small grid search over learning rate, weight decay, batch norm epsilon, and what epoch to decay the learning rate
Learning recurrent cells for Penn TreeBank
Control Experiment1: Adding more functions in the search space
E.g., add max function to combination functions; add sin to activation functions
Control Experiment1: Comparsion against Random Search
Conclusion
Code for running the models found by the controller will be released at https://github.com/tensorflow/models
the RNN cell found using our method under the name NASCell into TensorFlow
Also see in https://www.cnblogs.com/marsggbo/p/9347678.html