Introduction to Reinforcement learning

Posted on | In

强化学习

什么是强化学习

介于监督学习（有label）和无监督学习的中间

  • 没有监督信息，只有“奖赏”的反馈信号
  • 反馈通常是延迟的
  • 样本通常不符合独立同分布假设
  • 智能体的动作会影响到其后续观察到的数据的分布

Example：

  • 直升机的飞行控制
    • +r 沿着既定路线飞行
    • -r 偏离或坠毁
  • 组合投资管理
    • +r 盈利
    • -r 亏损
  • 电站的控制
    • +r 稳定输出电力
    • -r 超出安全预警
  • Atari游戏的控制
    • +r 增加游戏分数
    • -r 减小游戏分数

序列决策问题

奖赏 Reward

用于评价智能体在给定任务上动作的“奖励”：

  • 通常是一个标量
  • 在智能体决策的每一步，都会得到环境对其的奖赏
  • 智能体的目标是最大化累积奖赏

问题可以用强化学习建模：

​ 任务的目标可以等价的表示为在某个奖赏函数上的累积最大化

1
2
3
4
5
6
7
8
9
10
11
12
13
          ----观察o1---->
          <----动作a1----  
          ----奖赏r1,o2---->
环境      <----动作a2----    智能体
          ----奖赏r2,o3---->
          <----动作a3----
          ----奖赏r3,o4---->

$\max\sum_{i=1}^{T}r_i$

目标：

  • 通过选择动作最大化累计奖赏
  • 奖赏可能得到延迟
  • 有时需要牺牲眼前的小利益获得长远的大利益

状态 state

历史定义为，t时刻之前能观察到的所有信息：

$$ a_1, r_1,…o_t$$

状态是决定接下来会发生什么的关键信息

  • 环境状态 $S_t^e$
    • 环境的私有表示信息
    • 决定了下一步环境反馈什么观察和奖赏给智能体
    • 通常对智能体不是完全可见的
    • 即使完全可见，对智能体来说含有大量的冗余信息
  • 智能体状态$S_t^a$
    • 智能体的内部表示
    • 决定了下一步智能体选择什么动作
    • 通常是强化学习算法的输入
    • 其可以表示为历史的一个函数，即$S_t^a = f(H_t)$

马尔科夫决策过程

马尔科夫链：

Markov

一个状态是马尔可夫的，当且仅当

$$P(S_{t+1}|S_t) = P(S_{t+1}|S1, S2,…St)$$

给定现在，未来与历史无关

环境的状态$S_t^e, H_t$都是马尔可夫的

全部可观察性：

​ 当$o_t=s_t^a=s_t^e$时，我们便得到了一个马尔科夫随机过程（MDP）

马尔科夫过程 MP

Definition: A Markov Process(or Markov Chain) is a tuple(S, P) 状态空间和概率转移矩阵

  • S is a (finite) set of states

  • P is a state transition probability matrix

    $P_{ss’}=P{S_{t+1=s’}|S_t=s}$

马尔科夫奖赏过程 MRP

A Markov Reward Process is a tuple $(S, P, R, r)$

  • S is a finite set of states

  • P is a state transition probability matrix

    $P_{ss’}=P{S_{t+1=s’}|S_t=s}$

  • R is a reward function

    $R_s = E{R_{t+1}|S_t=s}$

  • r is a discount factor, $r \in [0,1]$

马尔科夫决策过程 MDP

A Markov Decision Process is a tuple $(S, A,P, R, r)$

  • S is a finite set of states

  • A is a finite set of actions

  • P is a state transition probability matrix

    $P_{ss’}^a=P{S_{t+1=s’}|S_t=s, A_t=a}$

  • R is a reward function

    $R_s^a = E{R_{t+1}|S_t=s, A_t=a}$

  • r is a discount factor, $r \in [0,1]$

Example

马尔科夫随机过程 MDP

$V(sunny) = E[\sum_{t=1}^Tr_t|S_0=sunny]$

$V(sunny) = E[\sum_{t=1}^\infty \gamma^tr_t|S_0=sunny]$

状态值函数

马尔科夫决策过程

策略(policy)的引入：状态到动作的映射

随机策略 $\pi(a|s)=P(a|s)$

确定性策略 $\pi(s)=argmax_aP(a|s)$

MDP的策略评估

状态值函数 V

从状态s开始，使用当前策略进行后续动作选择，得到的期望奖赏

$V^\pi(s)=E_\pi[\sum_{k=0}^\infty \gamma_k R_{t+k+1}|S_t=s]$

$V^\pi(s)=E_\pi[R_{t+1}+\gamma V^\pi(S_{t+1})|S_t=s]$ (递归表示)

状态-动作值函数 Q

从状态s开始，执行动作a，并使用当前策略进行后续选择

$Q^\pi(s,a)=E_\pi[{\sum_{k=0}^\infty \gamma^k R_{t+k+1}|s_t=s,a_t=a}]$

值函数转换关系 Bellman Expectation Equation

$V^\pi(s)=\sum_a\pi(a|s)Q^\pi(s,a)$

$Q^\pi(s,a)=R(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)V^\pi(s^{\prime})$

=>

$V^\pi(s)=\sum_a\pi(a|s)(R(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)V^\pi(s^{\prime}))$

$Q^\pi(s,a)=R(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)\sum_a\pi(a|s)Q^\pi(s^\prime,a^\prime)$

最优状态值函数

$$V^*(s)=\max_\pi V^\pi(s)$$

最优状态-动作函数

$$Q^*(s,a)=\max_\pi Q^\pi(s,a)$$$

  • 最优函数值决定了MDP中可以达到的最优性能
  • 当最优函数值已知时，该MDP已解
定义策略上的偏序关系

定理：对任意的MDP有

  • 至少存在一个最优策略$\pi^$优于或不差于所有其他策略，即$\pi^ \ge \pi, \forall \pi$
  • 所有的最优策略都可以取到最优状态值函数 $V^{\pi^}=V^(s)$
  • 所有的最优策略都可以取到最优状态-动作值函数 $Q^{\pi^}(s,a) = Q^(s,a)$
最优策略

最优策略可以通过最大化Q函数得到，即

$\pi^(s)=argmax_aQ^{\pi^}(s,a)$

  • 对于任意MDP，总是存在一个确定性的最优策略
  • 如果最优Q函数已知，则最优策略已知
最优值函数

Bellman最优方程

$$V^(s)=max_aQ^(s,a)$$

$$Q^(s,a)=R(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)V^(s^{\prime})$$

=>

$V^\pi(s)=max_aR(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)V^*(s^{\prime})$

$Q^(s,a)=R(s,a)+\gamma\sum_{s^{\prime}}P(s^{\prime}|s,a)\max_a\pi(a|s)Q^(s^\prime,a^\prime)$

  • 没有闭式解，没有一个式子可以直接解出来
  • 可以迭代求解：值迭代，策略迭代，Q-learning，SARSA

强化学习算法

基于模型的方法

方法概述：

​ 转移概率和奖赏函数未知，用函数逼近的方法拟合转移概率和奖赏函数，变成标准的MDP问题，然后使用DP planning方法求解

特点：

  • 模型拟合通常是收敛的
  • 并不保证拟合模型上的最优策略是真实的最优

代表算法：

  • Dyna, GPS

研究较少，因为大部分问题难以建模，转移概率和奖赏函数非常复杂

基于值函数的方法

方法概述：

​ 通过估计值函数来隐式得到策略

特点：

  • 最好情况下可以最小化Bellman误差
  • 非线性情况下通常不保证收敛

代表算法：

  • Q-Learning, TD
基于策略梯度的方法

方法概述：

​ 直接对目标进行梯度推导，通常是sample，执行梯度方法进行策略提升

特点：

  • 避免值函数估计带来的策略退化（并不是loss回归误差越小，策略越好）
  • 直接对目标进行优化

代表算法：

  • Reinforce, TRPO
Actor-Critic类方法

结合值函数，策略梯度的方法

方法概述：

​ 估计当前策略的值函数，并通过其来提升策略本身，通常是和策略梯度方法结合在一起

特点：

​ 同时结合了值函数和策略梯度

代表算法：

​ A3C

样本复杂度

model-based shallow RL -> model-based deep RL -> off policy Q-function learning -> actor-critic style methods -> on policy gradient algorithms -> evolutionary or gradient-free algorithms

more efficient (fewer samples) -> less efficient (more samples)

基于值函数估计的强化学习算法

过程

初始的Q值 -> 得到一个策略 -> 从环境中采样 -> Q值 ->…

fit $V(s)$ or $Q(s,a)$ -> set $\pi^(s)=argmax_aQ^{\pi^}(s,a)$

核心在估计值函数的计算/估计，第二步set较为简单

蒙特卡洛采样

Monte-Carlo Method:

$$Q^\pi(s,a)=\frac{1}{m}\sum_{i=1}^mR(\tau_i)$$

$\tau_i$ is sample by following $\tau$ after $s,a$, 采样的轨迹

多次采样，效率低，无法泛化

Monte-Carlo update:

$$Q(s_t,a_t)=Q(s_t,a_t)+\alpha(R-Q(s_t,a_t))$$

MC error: $\alpha(R-Q(s_t,a_t))$

增量更新，R从t+1开始，是轨迹上的，需要环境中run很多步，得到一个轨迹，到达终止状态或人为设置的步数，所以代价也很大

Temporal difference Method: TDerror

$$Q(s_t,a_t)=Q(s_t,a_t)+\alpha(r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t))$$

  • TD error: $r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)$

  • $R$ – $r_{t+1}+\gamma Q(s_{t+1},a_{t+1})$

    t+1之后的就不参加，用已有的Q估计代替，采样就只有一条

采样代价小，可泛化，参数化

Q-learning

$Q^\pi(s,a)$ based on $\pi$

$Q(s,a)$ $-\max_aQ(s,a)$

off-policy TD control

$Q_o=0$, initial state
for $i=0,1,..$

​ $s’,r$ = do action from policy $\pi_\epsilon$

​ $a’=\pi(s’)$

​ $Q^\pi(s,a)+=\alpha(r+\gamma Q^\pi(s’,a’)-Q(s,a))$

​ $\pi(s)=argmax_a Q(s,a)$

​ $s=s’, a=a’$

end for

目前在模型中学习到的policy

on-policy TD control

$Q_0=0$, initial state

for $i=0,1,…$

​ $s’, r$=do action from policy $\pi_\epsilon$

​ $a’=\pi_\epsilon(s’)$

​ $Q^\pi(s,a)+=\alpha(r+\gamma Q^\pi(s’,a’)-Q(s,a))$

​ $\pi(s)=argmax_a Q(s,a)$

​ $s=s’, a=a’$

end for

a是执行采样的policy得到的,$\pi_\epsilon$参数化的policy

  • off policy：able to improve the policy without generating new samples from that policy
  • on policy: each time the policy is changed, even a little bit, we need to generate new samples

如果空间连续，不能这样做

值函数估计

可以将Q用参数表示，w

Q-learning with function approximation

$w=0$, initial state

for $i=0,1,…$

​ $s’,r=$ do action from policy $\pi_\epsilon$

​ $a’=\pi(s’)$

​ $w+=$ $\theta(r+\gamma\hat Q(s,a)-\hat Q(s,a)) \nabla(s_t, a_t)$

​ $\pi(s)=argmax_a Q(s,a)$

​ $s=s’, a=a’$

end for

$J(w)=E_{s\sim\pi}[(Q^\pi(s,a)-\hat Q(s,a))^2]$

$\hat Q(s,a)$– when using DNN model, it will be Deep Q-learning(DQN)

基于策略梯度的强化学习算法

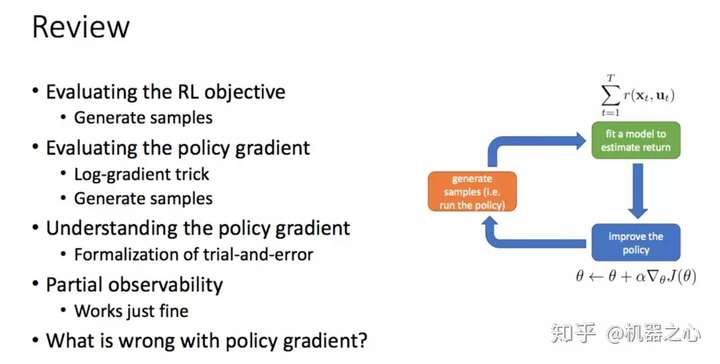
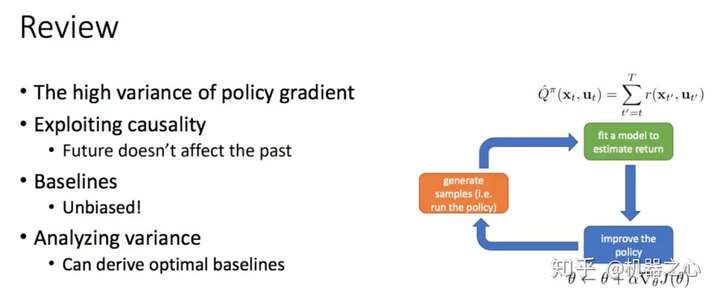
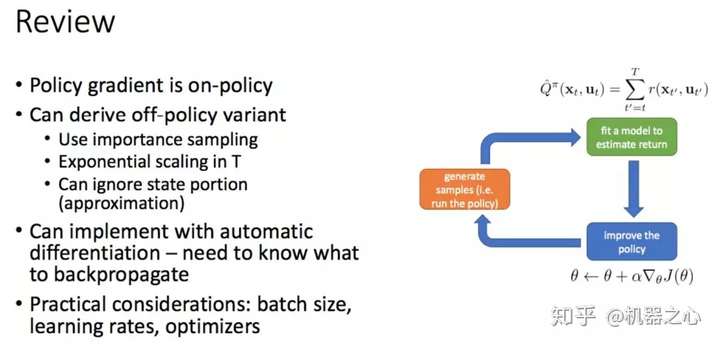
核心在梯度的计算

目标函数->梯度->优化

$$J(\theta)=\int_\tau {p_\theta(\tau)R(\tau)} \,{\rm d}\tau$$

$\theta$ , policy的参数，$J$ 是策略在所有轨迹$\tau$的概率的期望

$$P_\theta(\tau)=p(s_0)\prod_{i=0}^{T-1}p(s_{i+1}|a_i,s_i)\pi_\theta(a_i|s_i)$$

$\nabla_\theta J=\int_\tau {p_\theta(\tau)\nabla_\theta p_\theta(\tau) \log R(\tau)} \,{\rm d}\tau$

trick: $\nabla_\theta p_\theta(\tau) =p_\theta(\tau)\nabla_\theta\log p_\theta(\tau) $

$p\nabla_\theta\log p_\theta(\tau)=$ …

REINFORCE 算法

…

另一种表达（在稳定分布上积分）

…

A3C

DDPG

TRPO

PPO