Deep Residual Learning for Image Recognition
Q:Is learning better networks as simple as stacking more layers?
A:Noooo
An obstacle to answering this question was the notorious problem of vanishing/exploding gradients , which hamper convergence from the beginning .
This problem has been largely addressed by normalized initialization and intermediate normalized layers , which enable networks with tens of layers to start converging for SGD with bp.
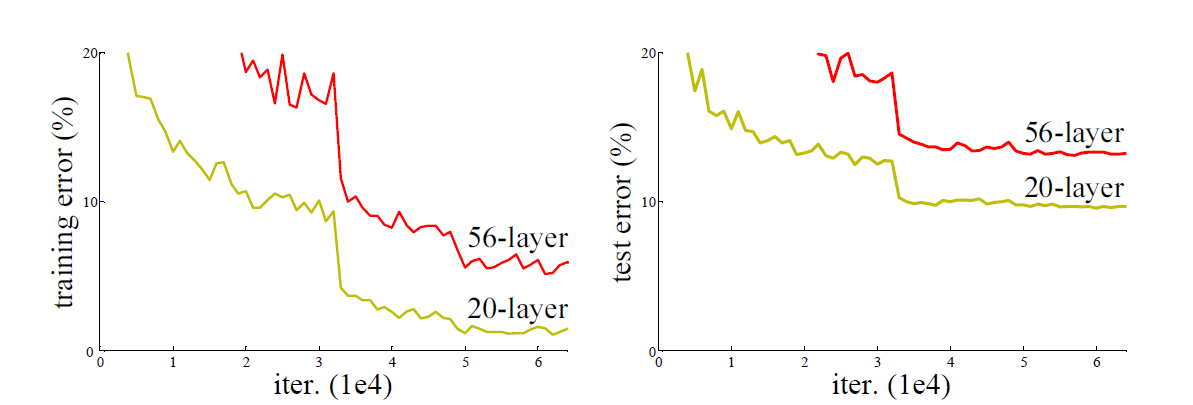
常规的网络的堆叠(plain network)在网络很深的时候,效果却却越来越差,train set和test set都变差。
产生这一问题的原因之一即 deeper network,gradients vanish越明显,network的训练效果也不是很好。
Resnet network的目标是在网络加深的情况下解决gradients vanish的问题。
method:
Plain_net:

Resnet network:
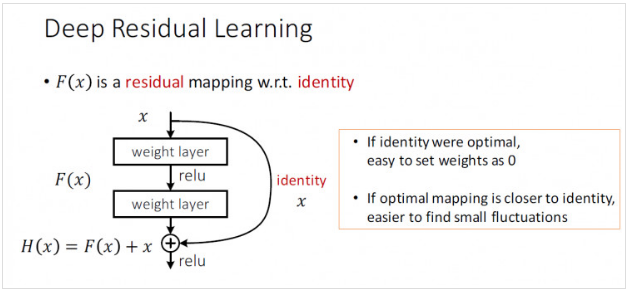
Identity mapping :X*I=X
20 layers -> 20 layers + 36 identity layers
There existence of this constructed solution indicates that a deeper model should produce no higher training error than its shallower counterpart .
shortcut connection :H(x)=F(x)+x,skip one or more layers
Results:
- Extremely deep residual nets are easy to optimize , but the counterpart “plain” nets(that simply stack layers ) exhibit higher training error when the depth increases
- Deep residual nets can easily enjoy accuracy gains from greatly increased depth , producing results substantially better than previous networks
Residual Network:
H(x) – an underlying mapping to be fit by a few stacked layers (not necessarily the entire net) , with x denoting the inputs to the first of these layers . 若干堆叠层将进行拟合的映射
If one hypothesizes that multiple nonlinear layers can asymptotically approximate complicated functions , then it is equivalent to hypothesize that they can asymptotically approximate the residual functions , i.e. H(x)-x
直接映射是难以学习的,提出了一种修正方法,不再学习x到H(x)的基本映射关系,而是学习这两种关系的差异,也就是残差residual,然后,为了计算H(x),我们只需要将这个残差加到输入上即可。
假设残差为F(x)=H(x)-x,那么网络不会直接学习H(x),而是学习F(x)+x
Identity Mapping by Shortcuts:
When the input and output are of the same dimensions ,
y=F(x,{Wi})+x,y and x are output and input vectors of the layers.
If not , 1)perform a linear projection Ws by the short connections to match the dimensions:y=F(x,{Wi})+Ws*x
2)The shortcut still performs identity mapping , with extra zero padded for increasing dimensions
如果输入和输出的维度不同,使用零填充或投射(通过1*1卷积)来得到匹配的大小